Benchmark Problems for Simulating
Electric Fields Near Triple Junctions
（３分岐近くの電界をシミュレートするベンチマーク問題）

Doug Craigen, PhD
Integrated Engineering Software/Enginia Research
Winnipeg, Manitoba, Canada R3H 0G4

見出し

: 問題; Boonchai Techaumnat 他による解; サンプルケース; まとめ

問題

電磁界シミュレーションの最も一般的な問題は、”最大値の大きさと場所”です。分岐があるとき、その問題は扱いにくくなります。左のサンプルケースでは、三分岐は誘電体（左）、空気（右）および電極（下部）です。電圧は良いように見えるが、この分岐は数学的には特異です。

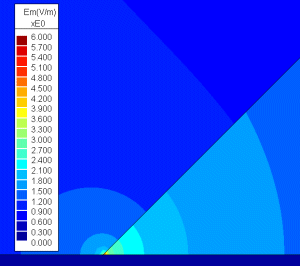その分岐でのフィールド方向を求めることはできません。それは分岐に近づく方向に依存します。さらに、フィールドの大きさはそのコーナーで無限大になります。そのため、コーナー近くのフィールドを調べると、次第に大きくなるフィールドになるべきです。その提示された質問は重要ではありません。何故なら、それはそのコーナーにどれだけ近づくか、およびどちらの方向から接近するか、に依存するからです。実際のフィールドは無限ではないというあなたの直感により、間違った解であると受け取ることは危険です。

正しい解を得ていることを確信するためには、ソルバーがその質問に対する正しい解を作成するかどうかを、決めることができるベンチマークを始める必要があります。

Boonchai Techaumnat他による解

接点付近の電場の振る舞いにおよぼす導電率の効果（PDF、英文）において、Boonchai他は次のようなケースを発表している：

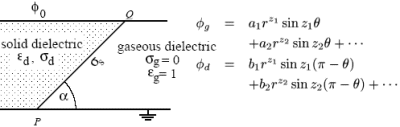
点Pの近くにおけるポテンシャル展開は r^numberの項の重ね合わせになり、その点に近づくほど、もっと多くの項がその解を支配することになります。その可能なnumberと支配的な最小の項を選ぶために、誘電体／空気のインターフェイスに沿って境界条件を使用しています。ポテンシャル式の勾配から電場Eを求めて、遠方場の一定値で正規化している。その結果は数値的なシミュレーションと非常に近くなっています。

サンプルケース

Based on Boonchai他の発見を元に、2D電界ソルバーELECTROにおいて、次のような問題を設定する：

そのモデルは、比誘電率=4および導電率=0を持つ、厚さ1m x 長さ20mの誘電体からなる。誘電体の上部は長さ40mで1Vの電極、および下部は長さ40mで0 Vの電極です。その内部が端部で半無限になるようにするために、２つの高さ1mの端部に0-1 Vの線形電位条件を与えています。

表示したメッシュは、以下でベンチマークするELECTROにある、２つの異なる解析オプション用です。

この問題で、可能なnumberの値は実数です。小数第６位でその最初のいくつかは、 0.80603, 2.00000, 3.19397 および4.80603である。rが小さいとき、0.80603の値が支配的になる。接点から離れた1V/mで正規化して、点Pの近くの誘電体中の電場Eを得る：

E_r = 0.80603 * r^(0.80603-1)sin(0.80603*theta)
E_theta = 0.80603 * r^(0.80603-1)cos(0.80603*theta)

ELECTROソルバーのスピードと精度を調べるため、４個の解析点が選ばれている：

(x, y)	E_r	E_theta
(0, 0.1)	1.2018 V/m	0.3780 V/m
(0, 0.01)	1.8785 V/m	0.5908 V/m
(0, 0.001)	2.9362 V/m	0.9234 V/m
(0, 0.0001)	4.5894	1.4433

最初の点を解くのは易しいが、解析点が３分岐の特異点に近づくにつれて、その解析は難しくなる。下に示したグラフは、様々なソルバー精度設定が、BEMおよび１次FEMソルバーでこれらの４点で得られた解析時間と値におよぼす効果を比較しています。

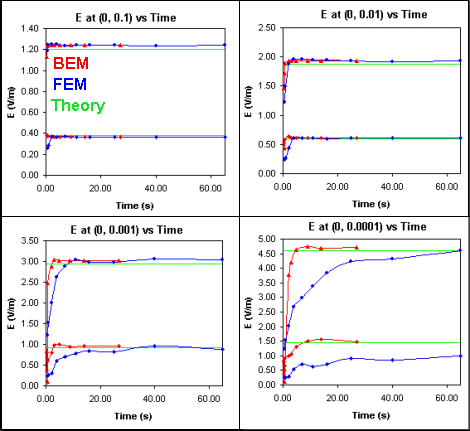
どちらの場合も、高精度の設定（解析時間が長い）がその分岐点近くの電場Eを得るために必要です。十分な高精度の設定に対して、どちらのソルバーもBoonchai他が予測した結果の数パーセント内に近づき、その理論とモデルの良い近似と考えられます。しかしながら、BEMソルバーはもっと早くその値に近づくことが可能です。BEMソルバーはFEMソルバーよりパフォーマンスが優れています。その理由は容易に理解できます。

下に示すFEM (上) and BEM (下)のメッシュを考える：

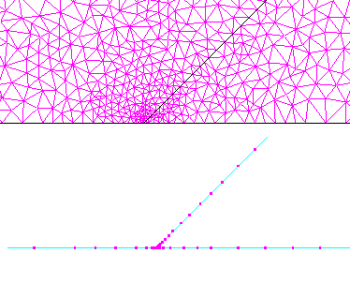
どちらのソルバーでも、分岐付近のフィールドがもっとも急激に変化するところを、より小さい要素を作成するように細かくすします。さらに精度の良い解を求めるときは、分岐付近の要素はより小さくなります。どちらのケースでも電場Eの空間解像度は、ローカルの要素サイズ程度です。BEMでは、そのメッシュは1Dであるので、２倍の要素を作成すると２倍ほど良い空間解像度が得られ、要素を10倍すると10倍の空間解像度、要素を100倍すると100倍の空間解像度が得られます。しかしながらFEMではそのメッシュが2Dであるので、２倍の要素を作成しても空間解像度はsqrt(2)=1.4の係数で改善され、要素を10倍にすると空間解像度はsqrt(10)=3の係数で改善され、要素を100倍にするとsqrt(100)=10の係数で改善されます。

空間解像度を要素サイズで調整し改善することは、BEMよりもFEMではより制限され、その違いは高解像度を得ようとするときもっとも効いてきます。実際、上の(0, 0.0001)のケースでの青色(FEM)の曲線を調べると、正確な解を知らなければ、その値が早く収束したと考えるような誤りをすることになります。

まとめ

３分岐付近の電場をベンチマークする解について、簡単な設定問題がBoonchai他により提案された。ここで、ひとつの具体的なケースを実行し、BEMとFEMの解にしばしば見られる食い違いについて研究しました。

次のような結論が示されている：

BEMとFEMの要素長さが求める点の付近で同じようなサイズであれば、その電場の解は同じになる。
BEMでは小さな要素を作ることはかなり容易なので、３分岐のような特異点付近で、BEMは少し大きい電場を予測する傾向にある。
FEMでは要素サイズは要素数の平方根で縮小するので、要素を増やして解の精度を上げるのが遅い傾向があり、それがその値が収束したという間違った印象を与える。
上の1), 2) と 3)により、３分岐まわりに何かある"最大値E"があるという考えは、通常使用する要素分布における弱点であり、作成したモデルの物理的な側面を表すものではない。
上の4)により、３分岐付近の"最大値E"を求めるために数値解法を使用する場合は、その問題を定義して解析する方法について注意する必要がある。接線に対して２つの材料の交差線がわずかに平坦になるというような小さなことが、明らかに分岐のすぐ近くでかなり違う結論を与えることを、理解する必要がある。また、その分岐にどのくらい近づくと特異になるか、その他のモデルの近似／仮定が調べられるかについて、合理的な判断基準を知る必要がある。

この研究に使用した計算機は、Windows 2000の2.4 GHzで実行しまた。

※開発元：Integrated Engineering Software