
ホーム > 最適設計 > OptiStruct > 機能
 OptiStruct 機能
OptiStruct 機能
 構造解析
構造解析
OptiStructは線形解析・非線形解析、静解析・動解析、モード解析、周波数ドメイン解析等、幅広い構造解析の問題に対応しています。
【スマートホンの三点曲げ】
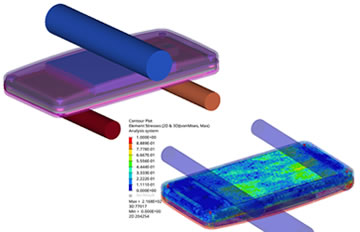
- 【構造解析機能】
- ・線形静解析
・線形座屈解析
・微小変位非線形解析
・大変位非線形静解析
・陽解法動解析
・直接法による過渡応答解析
(線形および非線形)
・ 固有値解析(実・複素)
・モーダル法による過渡応答解析
・ 周波数応答解析
・ランダム応答解析
・応答スペクトラム解析
 熱解析
熱解析
OptiStructは定常・過渡熱伝導解析および熱伝導率の温度依存性を考慮可能な非線形定常熱伝導解析に対応しています。また温度分布より応力分布を求める熱応力解析にも対応しています。
【熱解析】
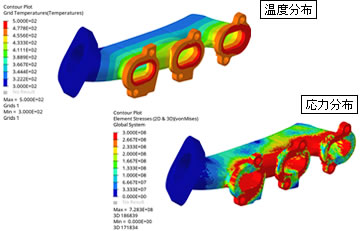
- 【熱解析機能】
- ・線形定常熱伝導解析
・線形過渡熱伝導解析
・非線形定常熱伝導解析
・熱応力解析
 疲労解析
疲労解析
OptiStructでは構造解析の結果を使用して、各種疲労解析を実施可能です。
【疲労解析】
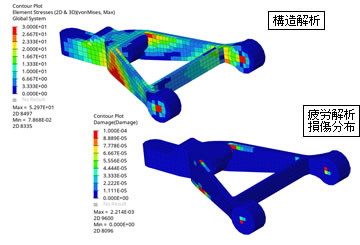
- 【疲労解析機能】
- ・単軸疲労解析
・多軸疲労解析
・ランダム応答疲労解析
・正弦波掃引疲労解析
・スポット溶接疲労解析
・シーム溶接疲労解析
 寸法最適化
寸法最適化
自動車部品などの様に板材によって構成される構造物に対して、部品ごとの板厚や断面形状を最適化する機能です。
【寸法最適化の例:自動車のフレーム部材】
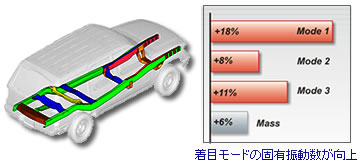
設計変数 : 各要素の板厚
目的関数 : 質量
制約条件 : 応力
- ・設計変数
- シェル板厚、ビーム断面形状
- ・特長
- 部材ごとに板厚、ビーム断面形状を決定できる
- ・用途の例
- 自動車のように板材の多い構造物
 フリー寸法最適化
フリー寸法最適化
場所によって板厚が変化する板材の構造物に対して、板厚分布を最適化する機能です。自動車の薄板など、様々な板材に対し適応可能です。
【フリー寸法最適化の例:航空機の構造部材】
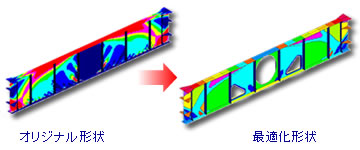
設計変数 : 各要素の板厚
目的関数 : 質量
制約条件 : 応力
- ・設計変数
- 各要素の板厚
- ・特長
- せん断パネルのような構造が得られる
- ・用途の例
- 航空機翼・胴体部のせん断パネル、自動車のボンネットインナーパネルなど
 形状最適化
形状最適化
メッシュを切り直すことなく、モデルの表面節点を指定した条件に従って移動させることにより形状を最適化する機能です。節点の移動はモーフィングと呼ばれる機能によりリメッシュすることなく任意の設定された方向へ移動が可能です。(パラメトリック)
例としては、以下の形状に対して目的に応じたパラメータを与える事で、最適化条件を定めます。
・軸の径を最適化 → 軸上の節点について、直径方向のみ移動させる
・部材の長さを最適化 → 部材上の節点について、長さ方向のみ変化可能
【形状最適化の例:パイプ材+ブラケット】
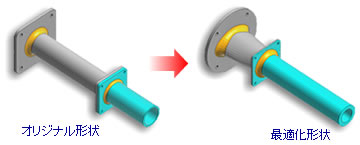
設計変数 : 節点位置
目的関数 : 質量
制約条件 : 応力
- ・設計変数
- 節点位置(ユーザーが移動の仕方を設定)
- ・特長
- 構造形状の変更の仕方を設定できる
- ・用途の例
- 径を変える、長さを変える、傾斜をつけるなど、構造形状の変更のパターンが既知の範囲で形状を決定するとき
 フリー形状最適化
フリー形状最適化
モデルの表面節点を自由に移動させることにより形状を最適化する機能です。(ノンパラメトリック)
節点が自由に移動するため、自由度が大きい形状最適化が可能な反面、現実的ではない形状が解となることもあります。そのため対称制約、型抜き制約などの製造性制約条件を与える事で現実的な解を得ることができます。
【フリー形状最適化の例:片持ち梁】
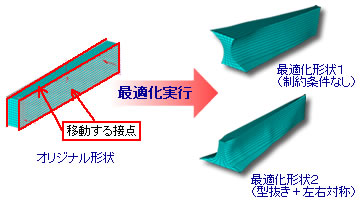
設計変数 : 節点位置
目的関数 : 質量
制約条件 : 荷重点変位
製造性制約条件の例
・左右対称にしたい
・任意の断面形状にしたい
・他の部品との干渉を避けたい
- ・設計変数
- 節点位置(自由な節点移動)
- ・特長
- 形状変更の自由度が高い
- ・用途の例
- 応力集中部位の形状検討など
 トポグラフィー最適化
トポグラフィー最適化
コストや質量を増加させることなく板材の剛性を高める方法としてビード、エンボスなどの加工があります。
このビード、エンボスの配置や形状を最適化する機能です。
【トポグラフィー最適化の例:シートベルト巻き取り装置ハウジング】
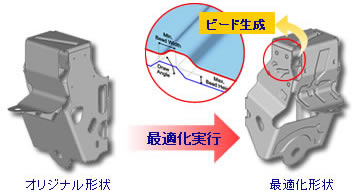
設計変数 : ビード生成位置
目的関数 : 剛性
制約条件 : ビード寸法
- ・設計変数
- ビード生成位置
- ・特長
- ビードの最適な配置を決定できる
- ・用途の例
- 板材にビード、エンボスなどの凹凸を生成させ、剛性、固有振動数を高くするとき
 トポロジー最適化
トポロジー最適化
最初に設計領域を材料で満たし、想定される荷重に対して材料が必要な場所と不必要な場所を要素密度コンターで表示する機能で、この結果を元に最適な形状を検討できます。
また、位相最適化とも呼ばれます。
例えば、リブ配置の検討で設計者の経験値に依存せず、解析に裏付けられた形状を得る事が可能です。概念設計の段階で、軽量化のためのデザイン検討をドラスティックにおこなう事ができ、従来とは異なる効率的で新しい部品形状を得る事が可能となります。
- ・設計変数
- 各要素の要素充填率(0~1 )
要素充填率が少ないとき、そこに材料は不要と判断する - ・特長
- 設計領域の材料配置を決定/ドラスティックなデザイン検討
- ・用途の例
- 概念設計での形状の検討など
【トポロジー最適化の例:ブラケット】
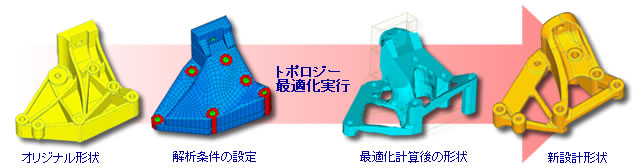
設計変数 : 各要素の要素密度
目的関数 : 質量
制約条件 : 応力
トポロジー最適化で得られた形状を基に、部品製造等も考慮した形状に再設計を実施
要求強度を保ちつつ、大幅な軽量化を実現!
© Terrabyte Co.,Ltd.



